使用OpenCV/python进行双目测距

2019年1月14日  2019年1月20日
qihong lu

步骤：

立体标定在另一篇文章已有教程这里直接从应用标定数据开始

我们所用到的主要函数stereoRectify以及initUndistortRectifyMap

Python: cv.StereoRectify(cameraMatrix1, cameraMatrix2, distCoeffs1, distCoeffs2, imageSize, R, T, R1, R2, P1, P2, Q=None, flags=CV_CALIB_ZERO_DISPARITY, alpha=-1, newImageSize=(0, 0)) -> (roi1, roi2)

参数：
  • cameraMatrix1 – 第一个相机矩阵。
  • cameraMatrix2 – 第二个相机矩阵。
  • distCoeffs1 – 第一个相机失真参数。
  • distCoeffs2 – 第二个相机失真参数。
  • imageSize – 用于立体校准的图像的大小。
  • R – 第一和第二摄像机的坐标系之间的旋转矩阵。
  • T – 摄像机坐标系之间的平移向量。
  • R1 – 为第一台摄像机输出3×3整流变换（旋转矩阵）。
  • R2 – 为第二个摄像机输出3×3整流变换（旋转矩阵）。
  • P1 – 在第一台摄像机的新（整流）坐标系中输出3×4投影矩阵。
  • P2 – 在第二个摄像机的新（整流）坐标系中输出3×4投影矩阵。
  • Q – 输出 4 \次4 视差 – 深度映射矩阵（参见参考资料 reprojectImageTo3D()）。
  • flags – 可能为零或的操作标志 CV_CALIB_ZERO_DISPARITY。如果设置了标志，则该功能使每个摄像机的主要点在整流视图中具有相同的像素坐标。并且如果未设置标志，则该功能仍然可以在水平或垂直方向上移动图像（取决于对极线的方向）以最大化有用图像区域。
  • alpha – 自由缩放参数。如果为-1或不存在，则该函数执行默认缩放。否则，参数应该在0和1之间。 alpha=0 意味着经过校正的图像被缩放和移位，以便只有有效像素可见（整流后没有黑色区域）。 alpha=1 意味着对经校正的图像进行抽取和移位，使得来自相机的原始图像的所有像素都保留在经校正的图像中（没有源图像像素丢失）。显然，任何中间值都会在这两种极端情况之间产生中间结果。
  • newImageSize – 整改后的新图像分辨率。应传递相同的大小 initUndistortRectifyMap()（请参阅stereo_calib.cpp OpenCV示例目录中的 示例）。当传递（0,0）（默认）时，它被设置为原始 imageSize。将其设置为较大的值可以帮助您保留原始图像中的细节，尤其是在存在大的径向扭曲时。
  • validPixROI1 – 整流图像内的可选输出矩形，其中所有像素均有效。如果 alpha=0，ROI覆盖整个图像。否则，它们可能会更小（见下图）。
  • validPixROI2 – 整流图像内的可选输出矩形，其中所有像素均有效。如果 alpha=0，ROI覆盖整个图像。否则，它们可能会更小（见下图）

 

Python: cv2.initUndistortRectifyMap(cameraMatrix, distCoeffs, R, newCameraMatrix, size, m1type[, map1[, map2]]) → map1, map2

参数：
  • cameraMatrix – 输入相机矩阵 A = \ vecthreethree {F_X} {0} {c_x} {0} {f_y} {c_y} {0} {0} {1}。
  • distCoeffs – （k_1，k_2，p_1，p_2 [，k_3 [，k_4，k_5，k_6]]） 4,5或8个元素的失真系数的输入向量 。如果向量为NULL /空，则假定零失真系数。
  • R – 对象空间中的可选整流变换（3×3矩阵）。 R1 或者 R2，计算方法 stereoRectify() 可以在这里传递。如果矩阵为空，则假定身份转换。在cvInitUndistortMapR中假设是一个单位矩阵。
  • newCameraMatrix – 新的相机矩阵 A '= \ vecthreethree {F_X'} {0} {c_x '} {0} {f_y'} {c_y'} {0} {0} {1}。
  • 大小 – 未失真的图像大小。
  • m1type – 可以是CV_32FC1 或 的第一个输出映射的类型 CV_16SC2。详情 convertMaps()请见。
  • map1 – 第一个输出映射。
  • map2 – 第二个输出映射。

 

 

根据以上代码我们只要输入对应参数即可，打开我们在Matlab保存的*.mat文件：

 

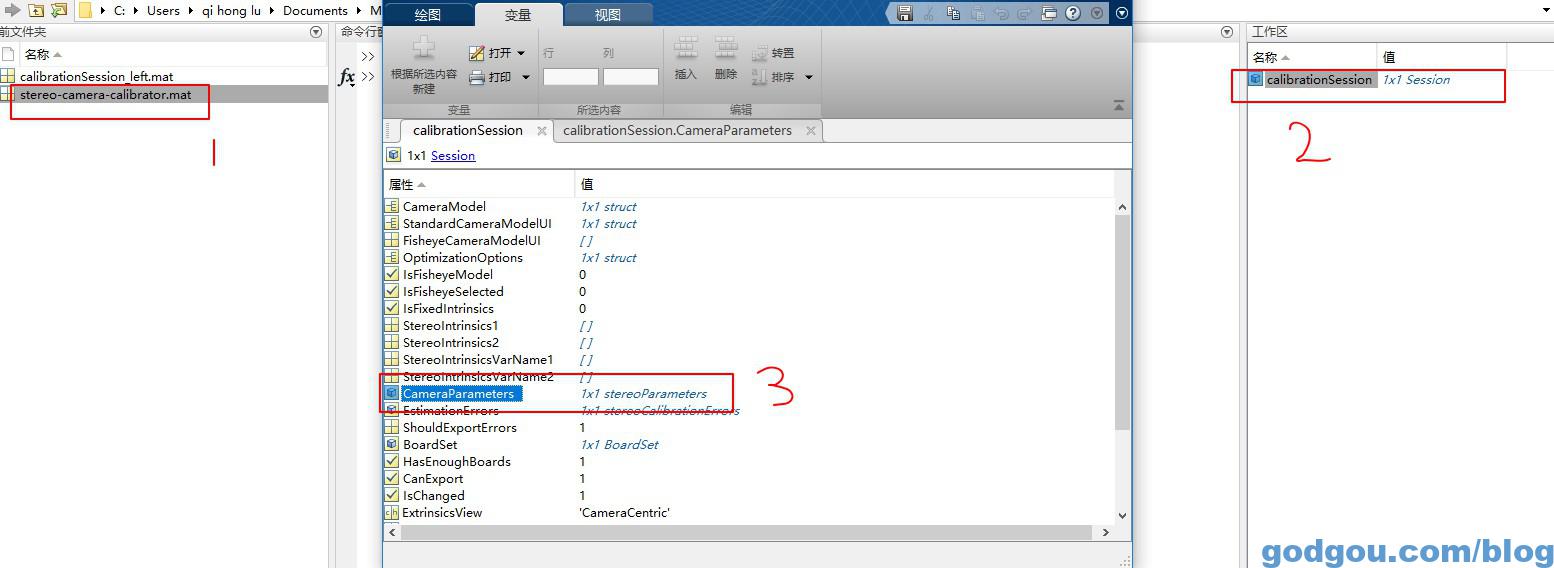
双击打开“CameraParameters ”得到如下文件：

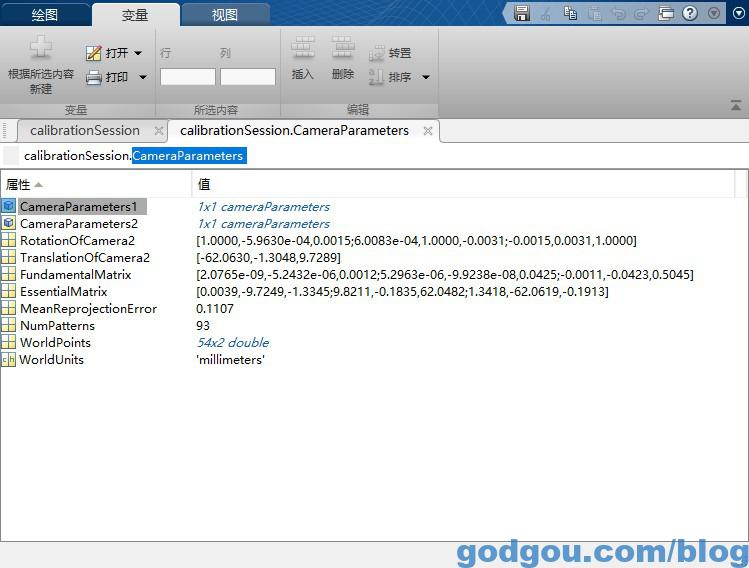
CameraParameters1一个相机矩阵就在里面拿

CameraParameters2第一个相机矩阵就在里面拿

RotationOfCamera2第二个相机相对于第一个相机的旋转矩阵3*3

如果你得到的是3*1向量可用如下代码转换为3*3距阵：
可以直接采用opencv中的Rodrigues函数实现，函数原型cv2.Rodrigues：

void Rodrigues( InputArray src, OutputArray dst, OutputArray jacobian = noArray() );
1
参数：
输入src：旋转向量（3*1或者1*3）或者旋转矩阵（3*3）；
输出dst：旋转矩阵（3*3）或者旋转向量（3*1或者1*3）；
输出jacobin：可选项，输出雅克比矩阵（3*9或者9*3），输入数组对输出数组的偏导数

TranslationOfCamera2摄像机坐标系之间的平移向量3*1

双击打开“CameraParameters1”如下图：

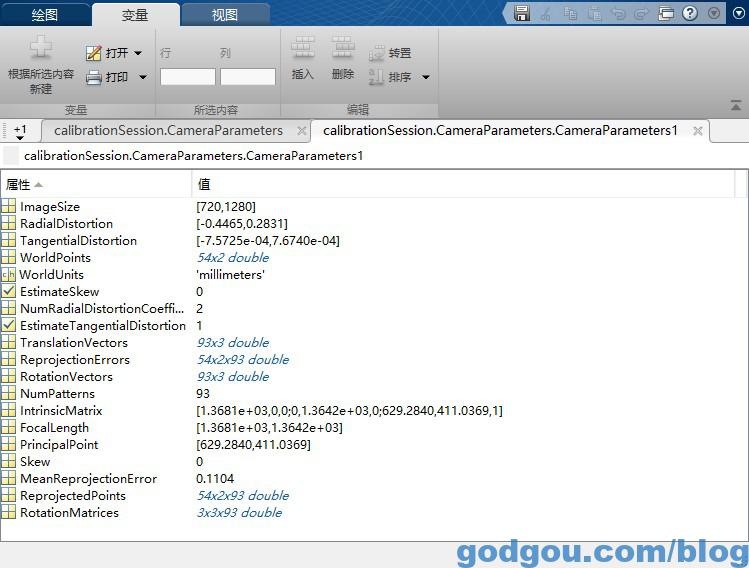
我们可以得到：

图像大小：ImageSize

失真(畸变)参数：RadialDistortion对应k1，k2，k3设置为0了所以上面只显示两个参数,TangentialDistortion对应p1，p2

在OpenCV中的畸变系数的排列（这点一定要注意k1，k2，p1，p2，k3），千万不要以为k是连着的。

相机内参：IntrinsicMatrix，注意这个和OpenCV中是转置的关系，注意不要搞错

我们标定出来的参数对应[fx,0,0;0,fy,0;cx,cy,1]但这里我们需要的参数格式为[fx,0,cx;0,fy,cy;0,0,1]

应用参数：

新建“mycamera_configs.py”文件完整代码如下：

 

转换深度图：

主要函数reprojectImageTo3D

Python： cv2.reprojectImageTo3D（视差，Q [，_3dImage [，handleMissingValues [，ddepth ] ] ] ） →_3dImage

参数：
  • disparity – 输入单通道8位无符号，16位带符号，32位带符号或32位浮点差异图像。
  • _3dImage – 输出与3相同大小的3通道浮点图像 disparity。每个元素 _3dImage(x,y) 包含(x,y) 从视差图计算的点的3D坐标 。
  • Q – 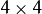4 \次4 可以获得的透视变换矩阵 stereoRectify()。
  • handleMissingValues – 指示函数是否应处理缺失值（即未计算差异的点）。如果handleMissingValues=true，那么具有与异常值相对应的最小视差的像素（参见StereoBM::operator()）被转换为具有非常大的Z值（当前设置为10000）的3D点。
  • ddepth – 可选的输出数组深度。如果是-1，输出图像将具有CV_32F深度。ddepth也可以设置为CV_16S，CV_32S或CV_32F。

该函数将单通道视差图转换为表示3D表面的3通道图像。也就是说，对于每个像素(x,y)和相应的差异d=disparity(x,y)，它计算：

\ begin {array} {l} [X \; Y \; Z \; W] ^ T = \ texttt {Q} * [x \; y \; \ texttt {disparity}（x，y）\; 1] ^ T \\ \ texttt {\ _ 3dImage}（x，y）=（X / W，\; Y / W，\; Z / W）\ end {array}

矩阵Q可以是任意 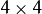4 \次4矩阵（例如，由计算的矩阵 stereoRectify()）。要将稀疏的点集{（x，y，d），…}重新投影到3D空间，请使用 perspectiveTransform()。

完整代码如下：

用鼠标点击即可输出当前点世界坐标，世界坐标系的原点是左摄像头凸透镜的光心

 

qihong lu
机器视觉

发表评论